The Weapon of Artillery

 WHAT IS WEIGHT OF FIRE?

Weight of fire concerns the quantity, density and intensity of artillery fire used to attack a target.  In essence it is about the effectiveness ('doing the right thing') and efficiency ('doing the thing right') of artillery fire at the target end.  The British undertook lots of research into this during World War 2 and in 1943 the War Office established the Fire Effect Committee.

BRITISH RESEARCH IN WORLD WAR 2

Broadly, research proceeded in two phases, initially theoretical investigations, experiments and trials in UK.  Then field studies by 1 Operations Research Section (ORS) in Italy and 2 ORS with 21 Army Group in NW Europe.  There are indications of some work in the Burma theatre but this seems to have been bequeathed to the Indian Government.  Studies examined hostile and fratricidal artillery fire, and friendly fire on subsequently captured positions.  Both sections had several artillery officers.  The morale effects were a particular concern and there was a lot analysis trying to separate this effect from the others, without much success.  

Initial work concentrated on HE fragmentation, the theoretical effectiveness of shells and the vulnerability of particular targets.  This being combined into usable data as ‘area of effect’ (AoE), originally called 'vulnerable areas', for each combination of shell and target type.  This led to such things as the definition of a casualty and, in contrast to the US, UK adopted a probability approach.  For example, “a 50% military loss occurs when a wound causes a disability lasting approximately 6 days” – the 100% loss was a 45-day disability.  This is a very good analytical approach and possibly valuable at the operational level but perhaps less useful as a tactical guide to units in the field.  

As an example of target vulnerability research, the mean presentation area of a human body across a variety of postures was calculated as 4.2 ft sq with vulnerable organs occupying 43% of the total at the front and 36% at the back.  Similar approaches can be used for equipment targets.

The Effects of HE Shells

The physical effects from High Explosive (HE) shells are caused by three things, in descending order of significance:

• Fragments or 'splinters' from the shell casing when it is shattered by the shockwave created by the detonating explosive filling, often erroneously called 'shrapnel'.  These fragments rely on kinetic energy for their effect.  A key point is that a high proportion of these fragments are wasted (they go up in the air or straight into the ground).
• Blast can be significant with very large calibre shells and all shells if they detonate in a confined space or very close (inches not yards) to a vulnerable hard target.  Blast is the pressure wave created by the expanding gases released from the fractured shell casing, it causes overpressure, which in turn causes damage.  When a shell penetrates the ground the gas pressure created by the detonation displaces material to form a crater.
• Flash from the heated gases, generally insignificant for artillery HE weapons, the blast and splinters will usually do more damage but flammable materials may catch fire.

Fragmentation

Shrapnel was widely used in World War 1, but not in World War 2, it was invented at the end of the 18^th Century.  In its 20^th Century form a time fuze detonated a propelling charge in a carrier shell with a low angle of descent to fire a few hundred balls (called bullets) forwards and downwards in a narrow cone, like a shotgun.   However, by WW2 HE shells, which had started appearing at the beginning of the century, had replaced shrapnel.  Like shrapnel bullets, shell fragment kinetic energy is the product of a fragment's mass and velocity (½(mass × velocity²)), given equal initial velocity heavier fragments travel further because they have greater 'carrying power'.   

The fragmentation of HE shells and fragment velocity varies depending on the amount and type of explosive, the design of the shell body and type of steel.  Key parameters are the ratio of explosive weight to shell body weight and the ratio of internal diameter (ie explosive content) to shell wall thickness.  

A fragment of 1/8 oz or more has a 50% probability of being lethal at 200 feet from the point of burst (providing it hits in the area of a vital organ). Of course actual fragment sizes vary quite a lot, see Table 1, in part due to the shape of the shell.  One indicator is the ratio 'diameter of the shell cavity'/'thickness of the shell wall', calculating this means ratios through lots of 'slices' of a shell to find the mean.  For 25-pdr this ratio was about 4, the ideal is about 10.  Fragments have more air resistance than streamlined rifle bullets,  so lose their velocity more quickly.  However, heavier fragments have more 'carrying power', but bigger fragments means less of them from a particular size of projectile, which reduces the likelihood of a hit.  Nevertheless, fragment's 'un-aerodynamic' shape means they are very efficient at transferring kinetic energy on impact with a soft material.  

By 1941 British research determined that the best size for an anti-personnel splinter was under 1/25 oz (ie about 1 gram), significantly less than the then existing designs.  The 1907 criteria, reputedly  developed by France, was a force of 58 ft-lbs to create an incapacitating wound; however, 58 ft-lbs actually appears to have been the German criteria (8 kg-m (or Newtons)), the French one being only 4 kg-m, albeit 19 kg-m for horses).  British research with small fragments suggested closer to 5 ft-lbs (0.7 Newtons of force or 6.8 Joules of kinetic energy ) was all that was needed, and that it was energy not force or momentum that was the key.  In contrast research into anti-aircraft ammunition before WW2 led to the 3.7-inch HAA HE shell being designed to produce 2.5 oz fragments.  Larger fragments travel further and have greater effect on 'harder' targets, but there are less of them.  For more details about shells see the Ammunition page. Joules/mm² are the modern measure of fragment lethality.

The following table shows the percentage and numbers of fragments of different sizes for different percentages of HE weight in 25-pdr shells, optimum anti-personnel fragmentation comes from shells with HE content at least about 25% of total weight, this was not achieved in WW2.  However, the amount of fragmentation varies quite significantly with the power and violence of the explosive used, which also affects its destructive effects.

Table 1 - Fragment Sizes and Quantities for HE Content
(1 oz = 28.35 grams)

Most British field artillery shells used standard engineering steel, '19-ton' yield strength; in contrast the US used '23-ton'.  Using normal as opposed to high strength steel made it easier to produce shells.  However, it also meant that shell walls had to be thicker to survive firing stresses (assuming similar safety margins), which left less volume for explosive filling.  One rule of thumb is that 19 ton steel allows 7% HE fill while 23 ton permits 15%.  Table 2 shows the HE percentage in some World War 2 shells and broadly supports this rule of thumb.  Note the weights are fuzed weights, a fuze typically weighed about 1 lb, contributed little to fragmentation and normally went into the ground.

Table 2 - Shell and Filling Weights
(1 lb = 0.453 kg)

This table shows the 4.5-inch shell was seriously deficient in explosive power having only about 3.8 lbs of HE, less than 105-mm!   However, given that the 4.5-inch Gun was primarily for counter-battery fire with the goal of damaging equipment then large fragments may not have been such a bad idea.

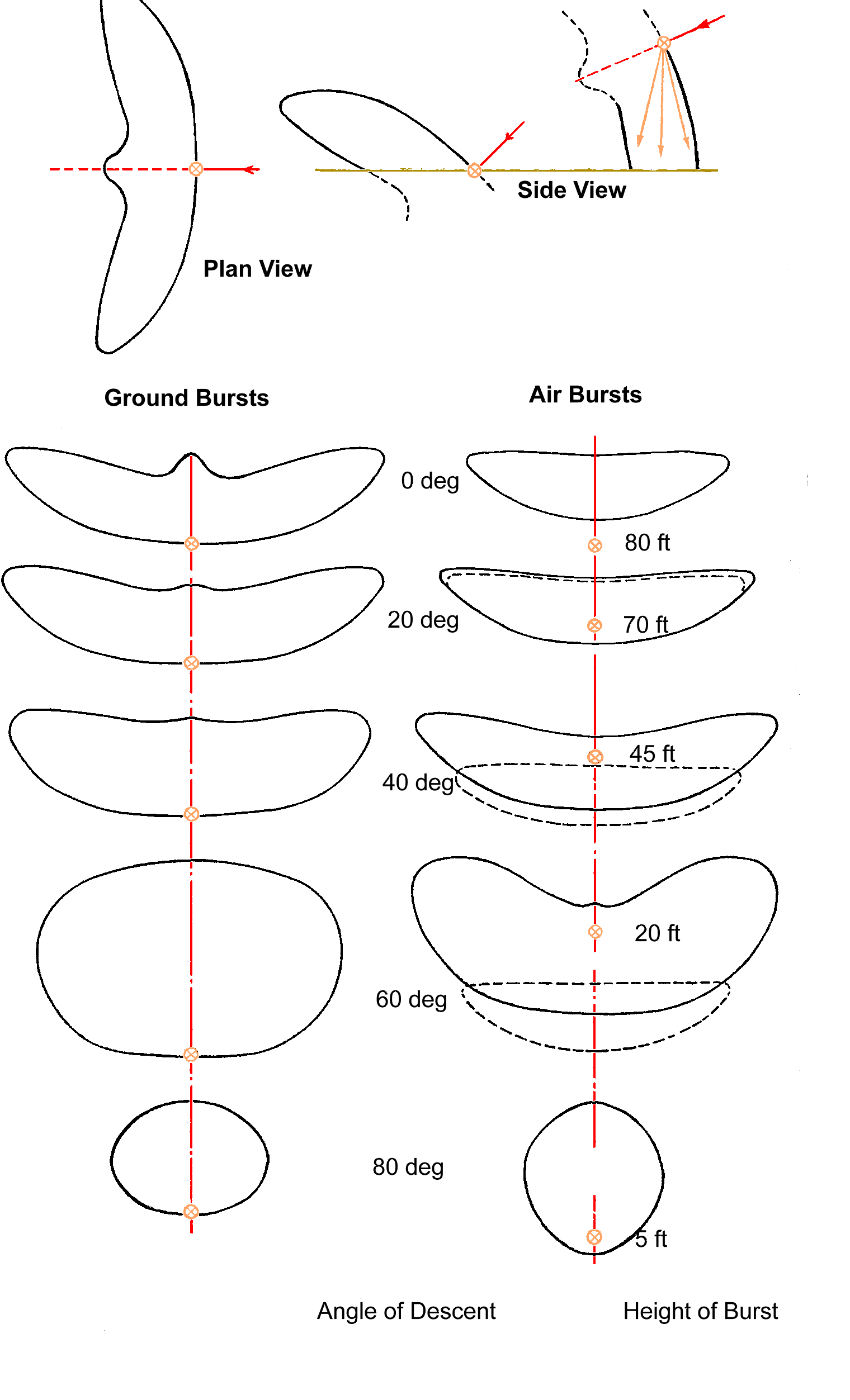
The pattern of the spread of fragments from an HE shell is shaped mainly by the fragment ejection angle and velocity (helped by shell rotational velocity), and modified by the terminal velocity and angle of descent of the projectile.  Most fragments from a static shell go in a direction of 90° from the external face of the shell body.  In flight shells 'wobble' and the angle of the external face varies in relation to the shell's long axis depending on its circular radius head (crh) shape.  However, the angle of descent is never vertical so a proportion of the fragments go into the ground or into the air and fall to earth by gravity.  More generally a typical angle of descent is 25° or less, and depending on the charge and range, terminal velocity is typically 25% - 35% of fragment velocity the nett effect (a vector sum) being to send the fragments about 25° forward of their static direction.  This gives a wing shaped pattern of the fragment spread.  Of course in all but the hardest ground even direct action fuzed shells penetrate a short distance, which which means the ground absorbs most of the forward projected fragments.  Figure 1 shows this in generalised plan view for ground burst shells of World War 2 type. Air-burst shells make use of the fragments projected downwards and the ideal anti-personal height of burst against troops in the open is 5 - 10 feet, which is difficult to achieve (even with VT fuzes due to the varying reflectivity of the ground) and was effectively impossible in WW2.  However, higher bursts are more effective against dug-in troops.  

Typically, from a stationary Britsh WW2 shell initial fragment velocity was 3000+ ft /sec, although in some directions they may be substantially less, this is considerably less than the explosive's velocity of detonation.  The proportion of fragments going forwards and backwards can vary substantially between shell designs, although those going forwards are often very small size; the base of the shell is usually much thicker that the side walls and often breaks into just a few large fragments that tend to go back along the trajectory.  However, a moving shell has two effects on fragments, first the terminal velocity, (for 25-pdr varying between 600 and 1000 ft/sec) imparts forward movement on the fragments.  Second, the surface of the spinning shell imparts its tangental velocity, (for 25-pdr varying between 90 and 230 ft/sec).  Fragments fly in straight-lines out from the shell burst but being un-aerodynamic in shape air resistance quickly retards them, despite their high velocity.  Gravity also pulls them down but by the time this is noticeable they have lost most of their kinetic energy.  Fragments going generally upwards fall to earth with little kinetic energy left.  

Figure 1 - Ground and Air Burst Fragmentation Patterns from the Point of Burst at Different Angles of Descent

The Effects of Terrain

The effects of terrain are many and varied and can markedly reduce the direct effects of bursting shells.  An impact fuzed shell will send its forward moving fragments into the ground.  In soft ground a shell will penetrate slightly deeper than in hard ground, this means that the crater will absorb more of the laterally projected  fragments.  Of course the efficiency of the fuze's instantaneous mechanism is a factor; inefficient impact fuzes penetrate deeper giving fewer useful fragments (this was a significant problem in the early part of World War 1 when 'graze' fuzes were used).  Of course penetration of  the ground may be required for destructive effects.  Graze fuzes,  direct action  fuzes with a delay mechanism  or direct action fuzes fired with 'cap on' could be used for this, and graze and 'cap on' was also used against targets behind light cover.

However, very few targets are on football fields.  'Normal' open ground is 'rough', it has natural folds, small dips and hollows, furrows, ditches, bunds, etc.  These all provide troops with protection from ground bursting weapons, not to mention direct fire projectiles.  'Natural' or 'average’ ground offers about 5 times as much protection to a prone soldier as an 'unnatural' level surface like a football field.  Then there are the more obvious results of human activity such as buildings and walls, and military activity, notably trenches.  However, air-burst shells direct their fragments into and behind this natural or artificial protection.

Buildings are a further complication, and their protective properties depend on the amount of artillery fire directed at them and the material used to build them.  The blast effect of shells will damage buildings, particularly if there are direct hits, and if there are enough hits the building will be reduced to rubble.  However, most masonry or concrete buildings will stop fragments.  The flash of detonation can ignite flammable materials in buildings.

Then there is vegetation.  Fragments and blast will strip away foliage and eventually reduce large trees to shattered trunks. The branches and trunks will absorb many splinters, one test for the 58 ft-lbs criterion was that a fragment penetrated about 1 inch into wood.  In heavy bombardments the blast will move the loose and shattered vegetation on the forest floor to the edge of the impact area or pile it up against obstacles such as large branches 'cut' from the trees.  However, before the trees are well stripped by shell fire the shells burst in the branches and are effective air-bursts.

Flying debris can be a hazard, particularly rubble in built up areas when large shells are used.  In either soft or hard ground artillery shells do not cause a noticeable hazard from flying spoil and forest debris usually offers little danger except at close range to the burst.  

British research also investigated using artillery fire to cut wire entanglements and clear mines, wire cutting had been a vital artillery task in WW1 before tanks arrived and trials were conducted in that war.  This work showed that there were some useful effects, blast being quite effective against some types of Teller mine and shell fragments easily cut wire.  However, they were not reliable or efficient methods due to the natural dispersion of the shells.

The Effects of Target Posture

It's also useful to note how vulnerability changes with target posture because it suggests the relative amounts of fire needed in different circumstances.  The following estimates the relative risks of becoming a casualty to ground-burst shells on ‘average’ ground:-

BATTLEFIELD EFFECTS

The direct effects of an HE shell are one way of looking at the effects of artillery fire.  However, they have to be related to the battlefield.  

British operational research scientists in WW2 defined artillery effects on the battlefield stating them “in order of their ease of achievement”, although they are all happening in some degree simultaneously.  They were:-

The last two, sometimes called “physical effects,” are much easier to analyse and in the final year of the war most of the research focused on the first two (“psychological effects”) through operations analysis.  The definition of demoralisation is particularly important; it is specific and is different from a more general deterioration in morale.  There was no information about recovery rates or how long the effect lasted.  There were additional caveats to demoralisation including that fire must be continuous over the period and that the target troops must not be fully protected against the bombardment by being in deep or concrete bunkers, etc.  Note to that “a lack of will to resist continuing for some time after the end of the bombardment” is different from the time taken for neutralised troops to decide that fire has ended and move to their fighting positions.

Of course there are also tertiary effects, notably disruption and delay caused by taking evasive or protective action, evacuating casualties and repairing damage, and so on.  And casualties will usually reduce, even if only temporarily, the efficiency and effectiveness of the unit suffering them, and may reduce capability if casualties or damaged equipment are not promptly replaced.  Note that here 'capability' is basically numeric strength in men and equipment and the target of attrition, efficiency is 'doing the thing right' and effectiveness is 'doing the right thing'.  Capability, effectiveness and efficiency all merge into combat power which reflects the human element and cohesion (morale, motivation and training), materiel (weapons and equipment) and the intellectual element (doctrine, concepts, tactics, techniques and procedures).

Quantitative Effects

British researchers put much effort into investigating and quantifying the effects of artillery fire.  The early focus was on physical effects.  Later work focused on the much more psychological ones, a much more challenging problem that was never entirely resolved.

Early work established splinter patterns and their relationship with the angle of descent and the all-important AoEs for different types of target.  Figure 2 shows an example of AoE contours.

Figure 2 – 25-pdr HE ground-burst, angle of descent 20º - Percentage Casualties to men standing in the open around the point of burst of the shell.

However, as Figure 1 shows, the shape of the fragment pattern depends on the shell's angle of descent, while the size of the AoE depends on the type of target and the lethality of the shell.  Nevertheless, data for shells, mortar bombs and aircraft bombs against various targets was provided and explained in Army Operational Research Group Report No 179 'Lethal and Material Effects of Gunfire and Bombing on Land Targets - A Record of the Present State of Knowledge' 20 March 1944.  It was updated in Report No 234, although the changes mainly concerned aircraft bombs, including relative areas for the blast effects of aircraft bombs.  It also considered the effectiveness of white phosphorus munitions, best summarised as 'not very'.

Next they produced estimated weights of fire to achieve these effects.  These are in terms of 25-pdr equivalence and shown in the next table.

Table 3 – Intensity and Density
 (1 yd = 0.9144 m, 1 lb = 0.453 kg)

*Note - The morale and neutralisation data need to be treated with caution; the evidence for achieving the defined demoralisation in 15 minutes was based on a single operation, at Wesel, during the Rhine crossings.  Before this it was thought that at least 4 hours were needed.  There is also doubt about 25-pdr effect equivalence for neutralisation because there were indications that neutralisation correlated with the number of rounds fired rather than their lethality.  

Equivalence Between Calibres

During World War 2 there were far more calibres than now so one need was relating the effects of one calibre of shell to another.  Using a standard target of 'men crouching in (British standard) slit trenches', a reasonable approximation of relative effect was the square root of the weight of explosive filling.  Of course this ignores the different power of different explosives and this type of target is one that is little affected by fragments. However, it is a representative target for an army on the offensive.  It also has logic, a splinter of a given size goes much the same distance no matter what size shell it came from unless there are very significant differences in the HE detonation velocity.  However, at any given distance from the burst there will be a greater density of fragments from a larger shell but this density decreases geometrically with distance.

Table 4 – World War 2 25-pdr Equivalence

25-pdr equals 1

A notable point is that smaller shells are proportionally more effective than larger ones.  However, the ratios aren't generally supported by the number of fragments derived from their distribution in Table 1.  Of course larger shells can be fired further, their greater explosive content makes them more effective against more solid targets, if they hit them, and their blast effects are greater.

What it Means on the Ground

Putting Tables 3 and 4 together reveals how many shells of different calibres are needed to achieve the different effects per 10,000 yds², ie 100 × 100 yds.

Table 5 - Density and Intensity per 100 × 100 yds
(8631 sq m)

An often asked question is about the effect of indirect artillery fire on tanks.  One example helps, in 1944 the German IX Corps in Italy reported that artillery fire was the largest single cause of its tanks losses, it seems that this was usually from medium and heavy guns controlled by air OPs.  The second largest source was German destruction of damaged or broken-down tanks to prevent their capture (mechanical reliability was not a feature of German tanks - but perhaps some of this was due to the Special Operations Executive's campaign of  insaisissable sabotage).  Other tanks, anti-tank, air attack and mines were well below the first two as the causes of tank losses.

CALCULATING WEIGHT OF FIRE AND FINDING THE RESULTS OF FIRE

Calculating density (rounds per 100 yd square) or intensity (rounds per 100 yd square per minute), involves two main steps:

• Finding the number of rounds to achieve the effect.
• Finding how many rounds to fire so that the necessary number hit the target.

Alternatively the same approach can be used to work out what results would have been for a given amount of fire.  The first step being to find how many shells probably hit the target and then what their result was.

Additional considerations include duration of intensity, the distribution of aim-points and the number of guns required.  The calculations are not absolute, like all gunnery they depend on statistics and probability theory.  However, before doing any calculations the data, AoE, has to be available for the expected target types and their postures.  Further data is also required as will be seen below.

Area of Effect

Figure 1, above, showed how AoE varies with the angle of descent and how a low angle pattern with its conspicuous ‘butterfly’ wings becomes more rounded as the angle steepens.

• The AoE becomes more circular as the angle of descent increases and the number of effective fragments increases because fewer are going into the ground or upwards before falling ineffectually.  
• Next, the AoE reflects a probability of effect in the area, not that any target element in the area will suffer the effect and that none outside it will.  
• Finally, the AoE definition may assume that a target in the open is on flat ground without any undulations, etc, providing cover against ground burst shells.

Unless direct hits are sought, HE air-burst is more effective than ground-burst for two reasons: for a given angle of descent there are more useful splinters, particularly at lower angles, and because the splinters strike downwards, instead of horizontally, they reach into holes and hollows.  Clearly, the extent of increased effectiveness will depend on the target.  Post World War 2 trials found that against dug-in targets proximity (VT) fuzed shells varied from about 1.2 to 2.5 times as effective as ground-burst.  However, some data from the war indicated that air-burst could be as much as 10 times as effective as ground-burst.  

One important aspect of air-burst is the height of burst (HOB), 30 feet was considered about optimal against troops in  trenches and if the bursts are too high then the effectiveness of the splinters is significantly reduced.  Getting this HOB by predicting the fuze length of 'time' fuzes, whether clockwork or powder burning, was virtually impossible so HOB had to be ranged.  Even with ranging the fuze to fuze variations and consequential spead of burst heights meant that there would be groundbursts.  The benefit of VT was its correct and consistent HOB without ranging it.  Of course against troops in the open ' daisy-cutters' are best but there was no prospect of achieving this with WW2 fuzes.

How many shells must hit the target to get the results?

The first step in weight of fire planning is calculating the number of shells to achieve the required effect on the target. For example:

• A target has 10 elements in an area 150 yds × 150 yds (22,500 yds²), the aim is to inflict a particular level of damage on any 4 of them (40%) and the AoE for this damage is 10 yds radius (314 yds²).
• Then N = P/100 × S/A, where N is the number of shells to be fired, P is the required percentage of damaged target elements, S is the target’s area and A is the AoE.  Here N = 29 (density 13 rounds per 100 yd square).

However, this simple model assumes that no target element will be hit effectively more than once.  This is statistically reasonable up to about 10% casualties, higher than this more shells need to be fired to compensate for ‘overhitting’, if 100% casualties are sought then the calculations must be for about 400%.  In the above example N should be 36 for 40% casualties.  A second assumption is that fire will be evenly distributed across the target, and in reality this was almost never the case in World War 2.  British practice was for a troop's guns to fire parallel and approximately in a straight line at right angles to their line of fire, of course the range probable error (PE_R) distributed the shells along each gun's line of fire but their 'average' impact was in a straightish line (depending on the accuracy of their relative calibration and assuming they were all firing with propellant from the same lot).  The overall spread improved when several widely separated regiments attacked a target.  See the 'Errors and Mistakes' page for more information about spread.

For example, modern thinking suggests that 30% casualties results in a target being militarily 'destroyed'.  The fine print of definitions and whether or not this is true are not considered further!  However, using the figures in Table 5, and the target of 'casualties to troops in weapon pits', suggest that for each 100 yds × 100 yds then 40 × 15 = 600 25-pdr shells were required.  Compensating this for overhitting raises the number to 690. 

When this is compared to the 8 - 32 shells per hour for neutralisation, then the implications of neutralisation versus destruction becomes clear, even without making allowance for shells that miss the target or are ineffective (see below).  Conversion factors in Table 4 can be used to convert to other types of shell.

AoE Shape

Another necessary adjustment is for the shape of the AoE.  This varies with angle of descent, which in turn varies with range and propelling charge size.  The problem of AoE shape is one of the keys to accurately estimating the extent of the effect on the target, and this was barely touched in the World War 2 work.

How many shells must be fired?

The second calculation step is to increase the theoretical number of shells to compensate for some of them missing the target or being ineffective.  There are several causes of this.  The first three concern 'accuracy' in a general sense.

Target Location Error – there is always some inaccuracy, although it's small for targets that have been effectively ranged (adjusted).

Accuracy of Fire – there are many possible causes of predicted fire inaccuracy - the distance between where the shells were aimed and their mean point of impact.  However, their magnitude at the target is closely related to range.  The work of the ORS identified lack of accuracy (errors) in predicted fire as a major problem, with incorrect muzzle velocities being particularly significant.  

Dispersion – the PEs in range and line, their size varies with range and charge.  Round to round variations in MV are the primary source of the first but there are various others including laying accuracy.  However, the importance of range dispersion depends on the size of the target and the relationship between the line of fire and the target axis.  Against larger target areas whose long axis is parallel to the line of fire dispersion may be a good thing, particularly at shorter ranges.

Slope – depending on the relationship between the direction of the slope of the ground and the line of fire, shells may fall outside the target area or not fully cover it.  1 ORS in Italy seem to have been the only group to incorporate this, no doubt because of its importance in the Italian terrain.

Angle of Descent - the shape of the AoE varies with the angle of descent and is relative to the line of fire.  So the line of fire and the shape of the effect may have more or less effect depending on the layout of the target, the relationship between the line of fire and the target's axis and the amount of dispersion.  Of course the angle of descent assumes horizontal ground, sloping ground with alter the effective angle of descent for fragmentation distribution purposes.

Blinds – there will always be some shells that don't explode.

Protective Qualities of Terrain - this is complicated and does not seem to have been included in WW2 calculation.  It also depends on the type of target.

The approach to the first three is to enlarge the target area to hold the PEs, typically combining them using root mean squares.  For adjusted fire the first two become a small PE depending on the adjustment precision.  Slope corrections make the target area asymmetric in relation to its ‘centre’.  Blinds are a percentage matter.  

Finally, considerations of accuracy and particularly dispersion, together with AoE shape come together with the relationship between the long axis of the target and the line of fire.  If the line of fire is across the axis of a long narrow targets far more rounds will be wasted than if the line of fire is along the target's axis.  This is because most dispersion is along the line of fire.

It will immediately be apparent that predicting compensation for accuracy, dispersion, AoE shape and slope again depends on where the guns are, and poses a real ‘chicken and egg’ problem if there is a choice of firing units.

Accuracy and dispersion, including dispersion compensating for inaccuracy, are reviewed in more detail in the "Errors and Mistakes" page.

How good are the calculations?

A key question is the goodness of the models.  British researchers summarised by an example giving the expected number of casualties as 9%.  They then said that it might be as low a 5% or as high as 15% but not as low as 2 or 3% or as high as 30 or 40%.  However, it could be argued that there is not, even today, a good model capable of handling all the variables and being used to either estimate the number of rounds required to produce the desired effects or reversible to estimate the effects for a given number of rounds.

Data quality is also an issue.  Physical effects are relatively easy to model and validate, although the latter may be expensive and apparently similar targets can vary widely in terms of their vulnerability.  Psychological effects are a different matter, realistic experiments and trials are out of the question on ethical grounds (at least in Western countries, although there are some tantalising hints that the Soviets may have experimented).  Therefore only war provides the data, but is not a good environment for well managed trials and experiments!

AFTER WORLD WAR 2

The need for more lethal HE shells was an important lesson from WW2.  UK fully developed two new shell designs during the early and late 1960's using higher strength steels.  105-mm Field (for Abbot) was about 1 kg heavier than the US 105-mm HE (1935 pattern) and was a slight improvement by having almost 16% HE.  155-mm for FH70 was a large improvement over HE M107, 26% instead of 15.8%.  Of course improvements in fragmentation were also achieved by changing HE fillings from predominantly TNT to RDX. The 21^st century change to plastic bonded explosives (with a RDX base) is again increasing the explosive power and improving fragmentation.  Some late 20^th Century multi-role fuzes, including those adopted by UK, offer height of burst options in their proximity (VT) function, this makes it possible match the height of burst setting to the ground so as to achieve the low air-burst or 'daisy-cutter', at 2 or 3 metres, which is best against some types of target.  

The training pamphlets covering the application of fire published in the late 1940's and early 1950's included very simple guidance.  The 1948 'Organisation, Command and Employment' pamphlet provided simplified data on bombardment intensity derived from the WW2 research. However, the 1952 'Engagement of Targets by Observed Fire' espoused the notion of 'immediate neutralization' achieved by 5% casualties and gave the numbers of rounds required to fall in a 100 yard square to achieve it.  Later training pamphlets ignored the subject apart from stating that the amount of fire was a matter of experience and judgement.  The source of this experience, for a peacetime army preparing for a war that was expected to last only days, was conveniently ignored.  

The matter lapsed until the 1980's when a requirement for weight of fire calculations was included in the Staff Requirement for BATES (Battlefield Artillery Target Engagement System).  This system adopted the US Superquickie II model for casualties and destructive effects, while neutralisation intensities were founded on UK WW2 data. The model was simple and originally designed to be run on an HP-41C programmable handheld calculator.  It was a reversible model (casualty % in & number of shells out or number of shells in & casualty % out), but ignored slope, the protective properties of the terrain and did not provide a variable shaping factor to represent the angle of descent, although it did include a 'factor k' (k = kludge).  The UK operational researchers had developed a model for casualty and destructive effects that accurately reflected the angle of descent.  However, it was not reversible and only gave casualty % for the number of rounds fired, which was not what was needed in the field.  It's  interesting to note that the Bundeswehr adopted Superquickie II for neutralisation by calculating 10% casualties and dividing by 60 to give rounds per minute intensity.

Copyright © 2001 - 2014 Nigel F Evans. All Rights Reserved.